MNIST Digits Recognition

Author

Mburu

Published

July 10, 2020

Read data and Load libraries

library(tidyverse)
library(data.table)
library(keras)
library(caret)
library(DT)
library(caretEnsemble)
library(tictoc)

train_data <- fread("data/train.csv")
set.seed(100)
N = nrow(train_data)
sample_one <- sample(N, 5000)
train_data <- train_data[sample_one]
test_data <- fread("data/test.csv")

Frequency of digits

ggplot(train_data, aes(x = factor(label))) +
    geom_bar()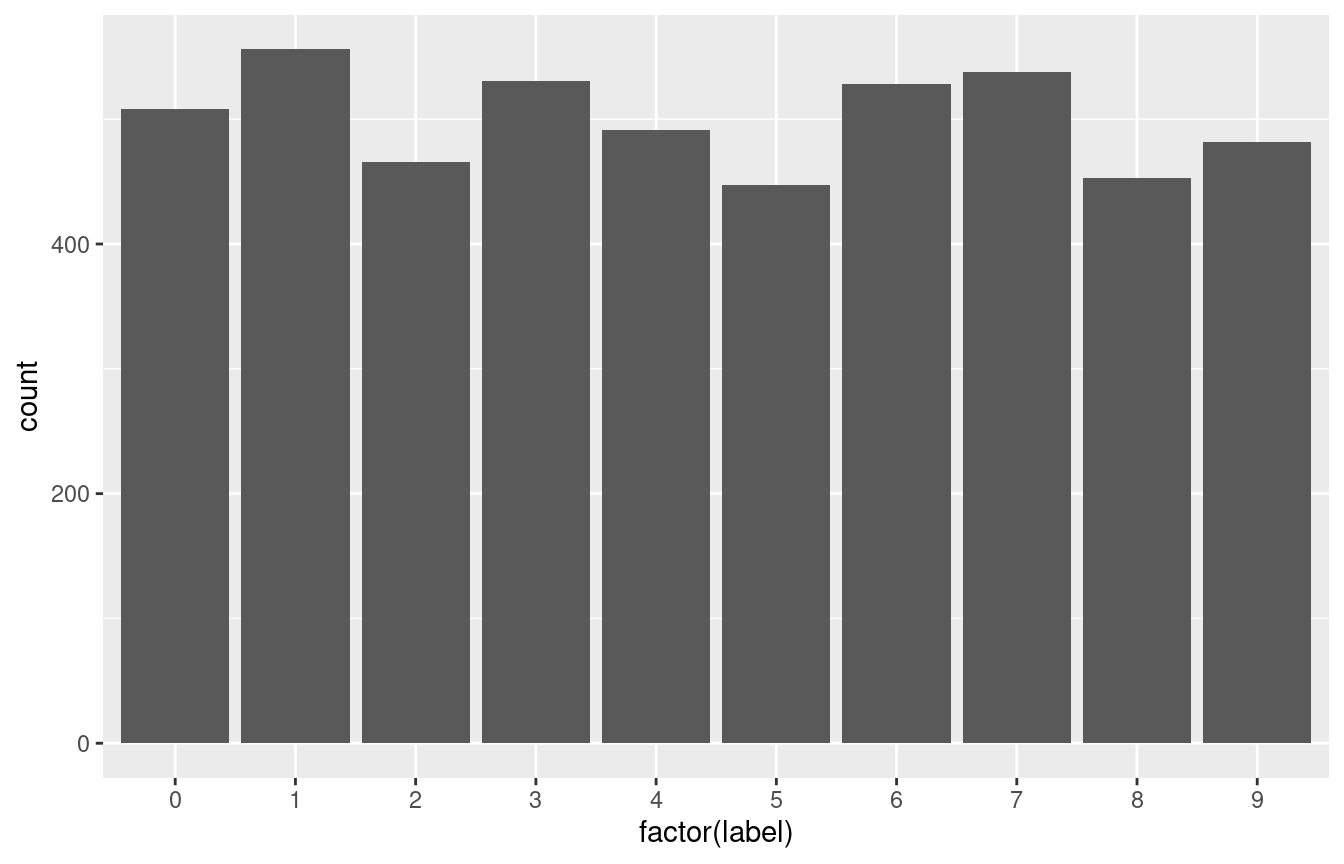

Randomly sample 12 digits

#  image coordinates
xy_axis <- data.frame(x = expand.grid(1:28, 28:1)[,1],
                      y = expand.grid(1:28, 28:1)[,2])


# get 12 images
set.seed(100)
sample_10 <- train_data[sample(1:.N, 12), -1] %>% as.matrix()

datatable(sample_10, 
          options = list(scrollX = TRUE))

sample_10 <- t(sample_10)

plot_data <- cbind(xy_axis, sample_10 )

setDT(plot_data, keep.rownames = "pixel")

# Observe the first records
head(plot_data) %>% datatable()

Plot 12 digits

plot_data_m <- melt(plot_data, id.vars = c("pixel", "x", "y"))

# Plot the image using ggplot()
ggplot(plot_data_m, aes(x, y, fill = value)) +
    geom_raster()+
     facet_wrap(~variable)+
    scale_fill_gradient(low = "white",
                        high = "black", guide = "none")+
    theme(axis.line = element_blank(),
                  axis.text = element_blank(),
                  axis.ticks = element_blank(),
                  axis.title = element_blank(),
                  panel.background = element_blank(),
                  panel.border = element_blank(),
                  panel.grid.major = element_blank(),
                  panel.grid.minor = element_blank(),
                  plot.background = element_blank())

Prepare data for model fitting

Decided to have a self test set

N = nrow(train_data)
sample_train <- sample(N, size = round(0.75 *N ))
test_own <- train_data[-sample_train]
train_data2 <- train_data[sample_train, ]
train_y <-to_categorical(train_data2$label, 10)

train_x <- train_data2[, -1]
#convert to matrix
train_x <- train_x %>%
    as.matrix()

train_x <- train_x/255

Construct model layers

model <- keras_model_sequential() %>%
  layer_dense(units = 784, activation = 'relu', input_shape = c(784)) %>%
  layer_batch_normalization() %>%
  layer_dropout(rate = 0.3) %>%
  layer_dense(units = 784, activation = 'relu') %>%
  layer_batch_normalization() %>%
  layer_dropout(rate = 0.3) %>%
  layer_dense(units = 392, activation = 'relu') %>%
  layer_batch_normalization() %>%
  layer_dropout(rate = 0.2) %>%
  layer_dense(units = 10, activation = 'softmax')

# Comp

Compile model

# Compile the model
model %>% compile(
  loss = 'categorical_crossentropy',
  optimizer = optimizer_adam(lr = 0.001), # Start with a default learning rate
  metrics = c('accuracy')
)

Fit model

# Implement a learning rate scheduler
lr_schedule <- function(epoch, lr) {
  if (epoch < 10) {
    return(lr)
  } else {
    return(lr * exp(-0.1))
  }
}

# Add the callback for the learning rate scheduler
callbacks_list <- list(callback_learning_rate_scheduler(schedule = lr_schedule))

# Train the model
hist <- model %>% fit(
    train_x, train_y, 
    epochs = 30,
    batch_size = 128,
    validation_split = 0.2,
    callbacks = callbacks_list
)

Epoch 1/30
24/24 - 1s - loss: 0.7792 - accuracy: 0.7577 - val_loss: 1.2017 - val_accuracy: 0.6920 - lr: 0.0010 - 1s/epoch - 54ms/step
Epoch 2/30
24/24 - 0s - loss: 0.2316 - accuracy: 0.9210 - val_loss: 0.9687 - val_accuracy: 0.7400 - lr: 0.0010 - 269ms/epoch - 11ms/step
Epoch 3/30
24/24 - 0s - loss: 0.1203 - accuracy: 0.9627 - val_loss: 0.7605 - val_accuracy: 0.8307 - lr: 0.0010 - 260ms/epoch - 11ms/step
Epoch 4/30
24/24 - 0s - loss: 0.0769 - accuracy: 0.9747 - val_loss: 0.6542 - val_accuracy: 0.8267 - lr: 0.0010 - 259ms/epoch - 11ms/step
Epoch 5/30
24/24 - 0s - loss: 0.0651 - accuracy: 0.9773 - val_loss: 0.6276 - val_accuracy: 0.8093 - lr: 0.0010 - 254ms/epoch - 11ms/step
Epoch 6/30
24/24 - 0s - loss: 0.0527 - accuracy: 0.9837 - val_loss: 0.4751 - val_accuracy: 0.8573 - lr: 0.0010 - 255ms/epoch - 11ms/step
Epoch 7/30
24/24 - 0s - loss: 0.0388 - accuracy: 0.9910 - val_loss: 0.3972 - val_accuracy: 0.8893 - lr: 0.0010 - 255ms/epoch - 11ms/step
Epoch 8/30
24/24 - 0s - loss: 0.0278 - accuracy: 0.9933 - val_loss: 0.3200 - val_accuracy: 0.9080 - lr: 0.0010 - 254ms/epoch - 11ms/step
Epoch 9/30
24/24 - 0s - loss: 0.0250 - accuracy: 0.9937 - val_loss: 0.3428 - val_accuracy: 0.9000 - lr: 0.0010 - 251ms/epoch - 10ms/step
Epoch 10/30
24/24 - 0s - loss: 0.0252 - accuracy: 0.9923 - val_loss: 0.2699 - val_accuracy: 0.9200 - lr: 0.0010 - 252ms/epoch - 11ms/step
Epoch 11/30
24/24 - 0s - loss: 0.0148 - accuracy: 0.9970 - val_loss: 0.2602 - val_accuracy: 0.9267 - lr: 9.0484e-04 - 255ms/epoch - 11ms/step
Epoch 12/30
24/24 - 0s - loss: 0.0146 - accuracy: 0.9973 - val_loss: 0.2578 - val_accuracy: 0.9267 - lr: 8.1873e-04 - 254ms/epoch - 11ms/step
Epoch 13/30
24/24 - 0s - loss: 0.0131 - accuracy: 0.9970 - val_loss: 0.2626 - val_accuracy: 0.9320 - lr: 7.4082e-04 - 255ms/epoch - 11ms/step
Epoch 14/30
24/24 - 0s - loss: 0.0143 - accuracy: 0.9973 - val_loss: 0.2580 - val_accuracy: 0.9320 - lr: 6.7032e-04 - 257ms/epoch - 11ms/step
Epoch 15/30
24/24 - 0s - loss: 0.0128 - accuracy: 0.9947 - val_loss: 0.2379 - val_accuracy: 0.9360 - lr: 6.0653e-04 - 256ms/epoch - 11ms/step
Epoch 16/30
24/24 - 0s - loss: 0.0111 - accuracy: 0.9973 - val_loss: 0.2523 - val_accuracy: 0.9373 - lr: 5.4881e-04 - 253ms/epoch - 11ms/step
Epoch 17/30
24/24 - 0s - loss: 0.0087 - accuracy: 0.9977 - val_loss: 0.2548 - val_accuracy: 0.9333 - lr: 4.9659e-04 - 257ms/epoch - 11ms/step
Epoch 18/30
24/24 - 0s - loss: 0.0104 - accuracy: 0.9977 - val_loss: 0.2530 - val_accuracy: 0.9387 - lr: 4.4933e-04 - 257ms/epoch - 11ms/step
Epoch 19/30
24/24 - 0s - loss: 0.0052 - accuracy: 1.0000 - val_loss: 0.2474 - val_accuracy: 0.9427 - lr: 4.0657e-04 - 255ms/epoch - 11ms/step
Epoch 20/30
24/24 - 0s - loss: 0.0046 - accuracy: 0.9993 - val_loss: 0.2475 - val_accuracy: 0.9387 - lr: 3.6788e-04 - 256ms/epoch - 11ms/step
Epoch 21/30
24/24 - 0s - loss: 0.0050 - accuracy: 0.9993 - val_loss: 0.2397 - val_accuracy: 0.9440 - lr: 3.3287e-04 - 256ms/epoch - 11ms/step
Epoch 22/30
24/24 - 0s - loss: 0.0067 - accuracy: 0.9990 - val_loss: 0.2428 - val_accuracy: 0.9480 - lr: 3.0119e-04 - 259ms/epoch - 11ms/step
Epoch 23/30
24/24 - 0s - loss: 0.0043 - accuracy: 0.9993 - val_loss: 0.2456 - val_accuracy: 0.9467 - lr: 2.7253e-04 - 255ms/epoch - 11ms/step
Epoch 24/30
24/24 - 0s - loss: 0.0042 - accuracy: 0.9990 - val_loss: 0.2488 - val_accuracy: 0.9493 - lr: 2.4660e-04 - 259ms/epoch - 11ms/step
Epoch 25/30
24/24 - 0s - loss: 0.0030 - accuracy: 1.0000 - val_loss: 0.2514 - val_accuracy: 0.9480 - lr: 2.2313e-04 - 252ms/epoch - 10ms/step
Epoch 26/30
24/24 - 0s - loss: 0.0038 - accuracy: 0.9997 - val_loss: 0.2507 - val_accuracy: 0.9467 - lr: 2.0190e-04 - 256ms/epoch - 11ms/step
Epoch 27/30
24/24 - 0s - loss: 0.0026 - accuracy: 1.0000 - val_loss: 0.2489 - val_accuracy: 0.9480 - lr: 1.8268e-04 - 253ms/epoch - 11ms/step
Epoch 28/30
24/24 - 0s - loss: 0.0038 - accuracy: 0.9990 - val_loss: 0.2530 - val_accuracy: 0.9467 - lr: 1.6530e-04 - 259ms/epoch - 11ms/step
Epoch 29/30
24/24 - 0s - loss: 0.0029 - accuracy: 0.9997 - val_loss: 0.2565 - val_accuracy: 0.9467 - lr: 1.4957e-04 - 257ms/epoch - 11ms/step
Epoch 30/30
24/24 - 0s - loss: 0.0036 - accuracy: 0.9997 - val_loss: 0.2558 - val_accuracy: 0.9467 - lr: 1.3534e-04 - 253ms/epoch - 11ms/step

plot(hist)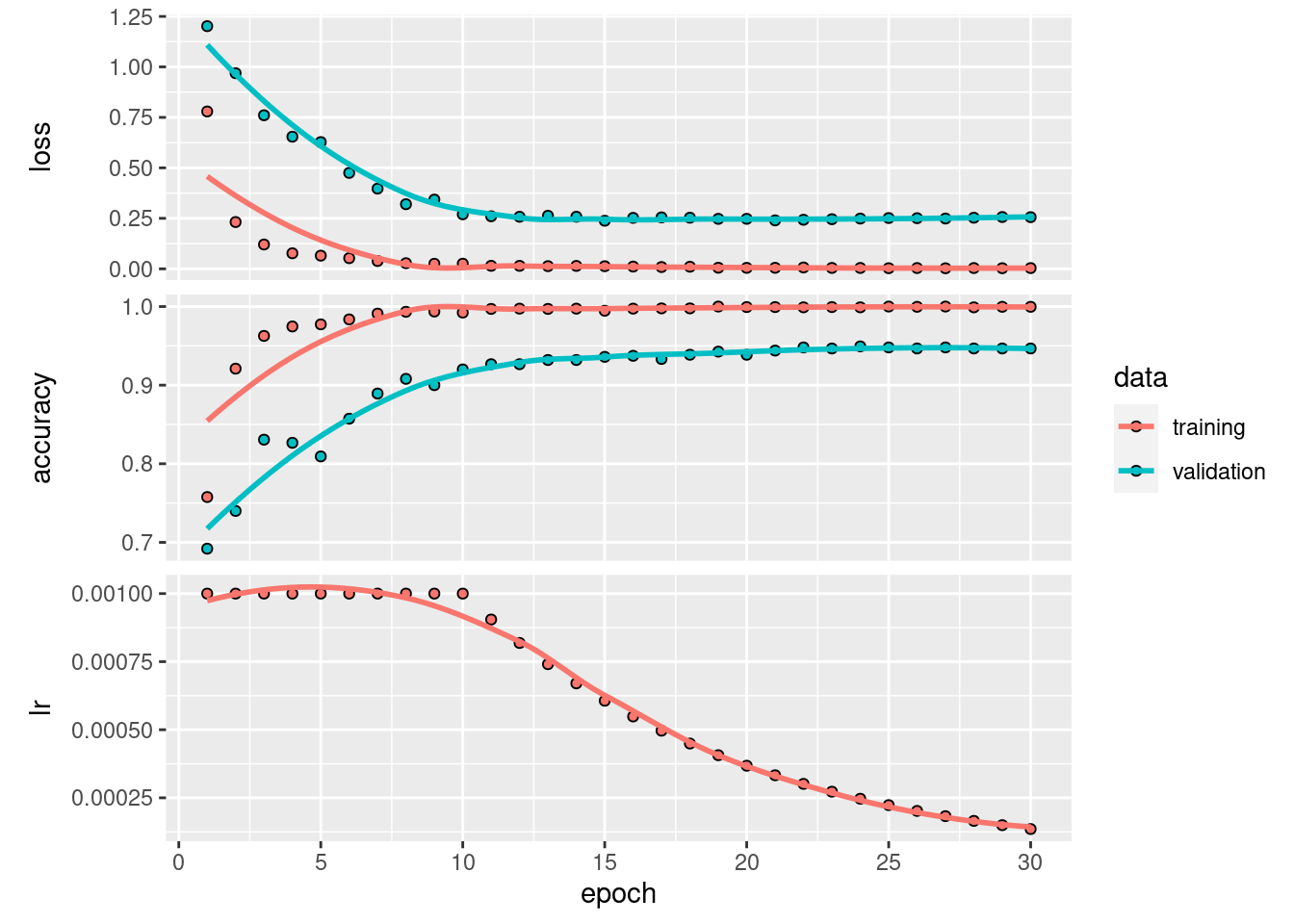

Own test

test_own_x <- test_own[, -1] %>% as.matrix()/255

test_own_pred <- model %>% predict(test_own_x)

40/40 - 0s - 146ms/epoch - 4ms/step

test_own_pred <- apply(test_own_pred, 1, which.max) - 1

confusionMatrix(data = factor(test_own_pred), reference = factor(test_own$label))

Confusion Matrix and Statistics

          Reference
Prediction   0   1   2   3   4   5   6   7   8   9
         0 122   0   1   0   1   0   0   1   0   1
         1   0 133   0   0   0   0   0   0   0   0
         2   0   2 104   1   1   0   0   0   0   0
         3   0   0   3 119   0   4   0   0   4   5
         4   0   1   0   2 118   0   0   0   0   4
         5   0   0   0   2   0  95   1   0   0   0
         6   0   0   0   0   0   1 147   0   1   0
         7   1   0   3   0   0   1   0 136   0   2
         8   2   0   1   3   0   1   1   0 111   1
         9   0   0   0   0   3   0   0   4   2 104

Overall Statistics
                                          
               Accuracy : 0.9512          
                 95% CI : (0.9378, 0.9625)
    No Information Rate : 0.1192          
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.9457          
                                          
 Mcnemar's Test P-Value : NA              

Statistics by Class:

                     Class: 0 Class: 1 Class: 2 Class: 3 Class: 4 Class: 5
Sensitivity            0.9760   0.9779   0.9286   0.9370   0.9593   0.9314
Specificity            0.9964   1.0000   0.9965   0.9858   0.9938   0.9974
Pos Pred Value         0.9683   1.0000   0.9630   0.8815   0.9440   0.9694
Neg Pred Value         0.9973   0.9973   0.9930   0.9928   0.9956   0.9939
Prevalence             0.1000   0.1088   0.0896   0.1016   0.0984   0.0816
Detection Rate         0.0976   0.1064   0.0832   0.0952   0.0944   0.0760
Detection Prevalence   0.1008   0.1064   0.0864   0.1080   0.1000   0.0784
Balanced Accuracy      0.9862   0.9890   0.9625   0.9614   0.9766   0.9644
                     Class: 6 Class: 7 Class: 8 Class: 9
Sensitivity            0.9866   0.9645   0.9407   0.8889
Specificity            0.9982   0.9937   0.9920   0.9921
Pos Pred Value         0.9866   0.9510   0.9250   0.9204
Neg Pred Value         0.9982   0.9955   0.9938   0.9886
Prevalence             0.1192   0.1128   0.0944   0.0936
Detection Rate         0.1176   0.1088   0.0888   0.0832
Detection Prevalence   0.1192   0.1144   0.0960   0.0904
Balanced Accuracy      0.9924   0.9791   0.9664   0.9405